Sostenibilidad y crecimiento
Por
José Enrique Villarino Valdivielso
Economista
Utilizar la palabra sostenibilidad se ha puesto de moda de un tiempo acá. No sólo en los medios científicos y universitarios sino también en las empresas. Todas las grandes corporaciones incorporan departamentos y direcciones de y para la “sostenibilidad”. Todas hablan de su sostenibilidad y la de sus productos y todas ellas dicen dedicar importantes recursos a ello. Se identifica sostenibilidad con el desarrollo sostenible a través de las ya tres clásicas líneas de actuaciones, la medioambiental, la económica y la social. Pero, realmente, por muy buenas intenciones y acciones que las naciones, las empresas y los individuos pongamos en hacer las cosas sosteniblemente, ¿es compatible un crecimiento constante con la sostenibilidad global del planeta? ¿No será una paradoja hablar de sostenibilidad en un mundo esférico y por tanto finito? ¿No será otra paradoja hablar de crecimiento contínuo –al que nadie quiere renunciar, tanto los que crecen como los que no- que afecta a procesos cuya naturaleza, cada vez más, son no lineales? Dicho de otra manera, que incrementos muy pequeños producen efectos muy amplios, muy grandes, en lapsos de tiempo muy cortos. Por otra parte, la cosa se complica todavía más si tenemos en cuenta que dichos procesos –sobre todo los ambientales- están muy interrelacionados. Esta etapa de la humanidad que nos ha tocado vivir se caracteriza frente a las pasadas en que casi nada es lineal y casi todo está interrelacionado con efectos acumulativos. Vivimos en la era de lo exponencial.
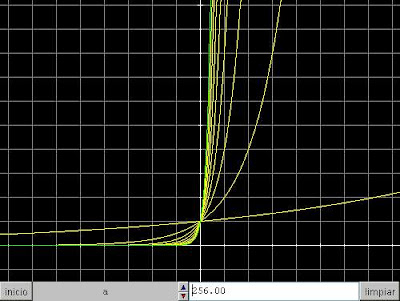 Para mejor hacernos una idea de ello, me he permitido grafiar una sencilla simulación exponencial usando una de las muchas páginas docentes de la red. El gráfico muestra las curvas de los ocho primeras lapsos de la función Y=2^x que no es sino la trampa que dice la leyenda que aquel sabio hindú le planteó a su monarca sobre el tablero del ajedrez, al solicitarle el doble del nº de granos de trigo por cada una de las 64 casillas del tablero de ajedrez. No había trigo en todo el mundo para colmar aquella sencilla y aparentemente humilde petición. Se trataba de una petición no lineal. Tampoco todo el trigo producido hasta entonces por la humanidad sería suficiente para satisfacer la petición. Así pues, sostenibilidad y crecimiento parecen ser cuestiones bastante incompatibles. El gráfico es expresivo por sí mismo. Si cada casilla del tablero fuese una unidad de tiempo –da igual cuál- al final de los 64 períodos, doblando se respecto del anterior, supondría –ojo- algo más de 13,8 TRILLONES de granos, personas, elementos, sucesos, o lo que sea. Basta ver la pendiente que alcanza la curva en el suceso octavo.
Para mejor hacernos una idea de ello, me he permitido grafiar una sencilla simulación exponencial usando una de las muchas páginas docentes de la red. El gráfico muestra las curvas de los ocho primeras lapsos de la función Y=2^x que no es sino la trampa que dice la leyenda que aquel sabio hindú le planteó a su monarca sobre el tablero del ajedrez, al solicitarle el doble del nº de granos de trigo por cada una de las 64 casillas del tablero de ajedrez. No había trigo en todo el mundo para colmar aquella sencilla y aparentemente humilde petición. Se trataba de una petición no lineal. Tampoco todo el trigo producido hasta entonces por la humanidad sería suficiente para satisfacer la petición. Así pues, sostenibilidad y crecimiento parecen ser cuestiones bastante incompatibles. El gráfico es expresivo por sí mismo. Si cada casilla del tablero fuese una unidad de tiempo –da igual cuál- al final de los 64 períodos, doblando se respecto del anterior, supondría –ojo- algo más de 13,8 TRILLONES de granos, personas, elementos, sucesos, o lo que sea. Basta ver la pendiente que alcanza la curva en el suceso octavo.
 Esta otra es la serie de la función Y(t)=(t-1)^2 en la que se observa el todavía mayor espectacular crecimiento que se produce a partir de la etapa siete, de tal manera que cada suceso es igual al cuadrado del anterior, que en la observación décima alcanza los casi 35.000 millones de unidades habiendo arrancado de 1,1 unidades en la observación nº 2.
Esta otra es la serie de la función Y(t)=(t-1)^2 en la que se observa el todavía mayor espectacular crecimiento que se produce a partir de la etapa siete, de tal manera que cada suceso es igual al cuadrado del anterior, que en la observación décima alcanza los casi 35.000 millones de unidades habiendo arrancado de 1,1 unidades en la observación nº 2.
Albert Bartlett es profesor emérito de la Universidad de Colorado en USA y es un firme defensor de algo que no está muy de moda y que ya allá por los inicios de los 70 puso de relieve el Club de Roma: la necesidad de los límites “al” crecimiento –no como se ha extendido “del” crecimiento-. Si ya entonces era necesaria la advertencia, que será hoy …. El profesor Bartlett ha divulgado un vídeo que FTF recoge en este post que tiene por título “Aritmética, Población y Energía” que trata de estas cosas y del poco caso que hacemos a la función exponencial, cuya visualización recomiendo. Porque quizá, con muchas papeletas y una muy alta probabilidad, estamos ya en el umbral de una era, cuyos efectos nefastos sobre el planeta y las especies que lo habitamos son irreversibles, sin retorno. El dilema ya no es crecimiento versus sostenibilidad. El dilema es, decrecer o decrecer.



No hay comentarios:
Publicar un comentario